Représentation mathématique de l'espace et du temps

En physique, l'espace-temps est une représentation mathématique de l'espace et du temps comme deux notions inséparables et s'influençant l'une l'autre. Cette conception de l'espace et du temps est l'un des grands bouleversements survenus au début du XXe siècle dans le domaine de la physique, mais aussi pour la philosophie. Elle est apparue avec la relativité restreinte et sa représentation géométrique qu'est l'espace de Minkowski ; son importance a été renforcée par la relativité générale.

L'espace-temps comporte quatre dimensions : trois pour l'espace, x, y, et z, et une pour le temps, t multiplié par la constante c (célérité de la lumière dans le vide). Un évènement se positionne dans le temps et l'espace par ses 4 coordonnées qui dépendent du référentiel. Le temps n'est pas le même suivant le référentiel dans lequel on le mesure, de même pour l'espace : la longueur d'un objet peut être différente selon le référentiel de mesure. Dans l'état actuel des connaissances, seul l'espace-temps comme concept unifié, est invariant quel que soit le référentiel choisi, tandis que ses composantes d'espace et temps en sont des aspects qui dépendent référentiel. Ce qui unifie espace et temps dans une même équation, c'est que la mesure du temps peut être transformée en mesure de distance (en multipliant t, exprimé en unités de temps, par c), et t peut donc de ce fait, être associé aux trois autres coordonnées de distance dans une équation où toutes les mesures sont en unités de distance. On peut dire que le temps, c'est de l'espace. La culture inca ne distingue pas l'espace et le temps ; l'espace-temps est appelé « pacha », en quechua.

Source : fr.wikipedia.org

Les maths sont une disposition d'esprit

Les mathématiques sont une attitude mentale qui se construit très tôt, lors de la découverte des formes, des quantités, de l'espace et des situations opératoires. Le programme scolaire de maths s'appuye sur les compétences de base qui ne sont pas assurée et tout l'édifice s'empile de manière fragile et trop peu étayée. Le problème n'est pas tant de résoudre l'opération, les élèves savent le faire, mais de savoir quelle opération il faut poser et c'est cela qui manque aux élèves.

Les mathématiques sont appréhendées, dès la petite section de maternelle avec des fiches. Colorier des formes identiques, colorier un nombre donné de formes, pourtant les enfants de trois à quatre ans apprennent principalement avec leurs corps et leurs sens, en manipulant, en expérimentant ce que préconisaient Pierre-Gilles de Gennes, Georges Charpak et « La main à la pâte ».


Lire l'article de Pierre Duriot sur atlantico.fr

Le ver crée une partition invisible

L’éditeur de solutions de sécurité Kaspersky décrit le groupe de hackers, baptisé groupe Equation, comme l’un des groupes de cyber-attaque les plus sophistiqués au monde. Spécialisée dans le cyberespionnage, cette entité opère depuis 2001, et peut-être même depuis 1996, à l’aide de malwares. Ces hackers ont notamment exploité deux vulnérabilités zero-day (c'est-à-dire qui ne sont pas connues de l’éditeur ou pas corrigées) identifiées dans le ver Stuxnet bien avant que ce dernier ne soit déployé. Selon l’éditeur russe, plusieurs dizaines de milliers de victimes ont été la cible d’Equation dans plus de trente pays. Ce malware se propage via une clé USB infectée dans laquelle le ver crée une partition invisible qui contient les commandes de contrôle ainsi que les données dérobées. Lorsque la clé USB est insérée dans un ordinateur ayant accès à l’Internet, elle transmet ses données et reçoit de nouvelles commandes.

Les chercheurs sont tombés sur un outil à la fois fascinant par sa complexité et totalement effrayant par sa puissance. Il s’agit d’un module identifié sous le nom de « nls_933w.dll » grâce auquel les assaillants peuvent reprogrammer le microgiciel d’un disque dur ou SSD. Ce module crée un espace invisible sur le système de stockage qui résiste à un formatage de niveau militaire. Les données dissimulées sont toujours disponibles pour l’assaillant, même après le formatage du disque dur et la réinstallation du système d’exploitation. Une fois qu’un disque dur ou SSD a été infecté, il est impossible de détecter ou de supprimer ce module malveillant.

Source : futura-sciences.com

11111011111

1024 + 512 + 256 + 128 + 64 + 16 + 8 + 4 + 2 + 1 = 2015, il manque 32 dans la liste des puissances de deux pour qu'elle soit complète jusqu'à 1024.
La formule élégante aurait comporté toutes les puissances de deux : 1024 + 512 + 256 + 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 2047, plus que 32 ans à attendre, 2047 sera THE real year.

L'écriture en puissances de deux donnée ci-dessus conduit à l'écriture binaire suivante pour 2015 :
11111011111
Et là, merveille, c'est justement parce qu'il manque 32, l'épine dorsale du milieu, cruel manque se traduisant par un zéro unique — laissant cinq chiffres 1 à sa droite (les puissances de deux de 0 à 4) et cinq autres à sa gauche (les puissances de deux de 6 à 10) —, que l'écriture binaire de 2015 est un palindrome.

Source : moatti.blogs.sciencesetavenir.fr

L'économie, une science humaine et sociale

Jean Tirole est devenu lundi dernier 13 octobre le Nobel d'économie 2014. Le magazine scientifique SCIENCES ET AVENIR rediffuse sur son site une interview d'octobre 2011.
L’économie utilise aujourd’hui l’outil mathématique de façon massive. Pourtant, selon vous, il s’agit d’une science humaine et sociale. Pour quelle raison ?
Il est vrai qu’il n’existe pour ainsi dire plus d’économie sans mathématiques ! Mais elle est incontestablement une science sociale, au même titre que la psychologie, la sociologie, le droit, la science politique… pour la bonne raison qu’elle décrit des comportements humains.
ce qui m'a attiré vers l’économie, c'est cette combinaison de rigueur mathématique et de comportements humains. Lycéen, je lisais beaucoup de livres d’histoire et de sociologie. J’appréciais Claude Lévi-Strauss et Marcel Proust qui analysaient parfaitement les petits jeux auxquels nous jouons avec les autres et avec nous-mêmes.

Qu’est-ce que la théorie des jeux, très en vogue aujourd’hui ?
Il s’agit d’analyser les choix faits par les acteurs, tous interdépendants, dans une situation donnée. Par exemple, nous nous interrogeons sur la façon dont les concurrents vont réagir si une entreprise décide de baisser ses prix. Nous raffinons l’analyse grâce à une théorie connexe, dite théorie de l’information. En effet, un acteur donné ne sait pas toujours exactement de quelle information dispose ses concurrents ! Or, cette donnée est capitale pour prendre des décisions. J’ai beaucoup exploré et approfondi la théorie des jeux, notamment avec Eric Maskin. Nous avons défini la notion « d’équilibre de Markov parfait » qui montre qu’on peut toujours identifier une variable– comme la part de marché d’une entreprise ou sa capacité de production, l’endettement d’un Etat, etc. – qui synthétise à elle seule toute l’histoire d’un jeu, et qui permet de prévoir ce que seront les stratégies des acteurs.

Idée déconcertante pour les non-mathématiciens

L’idée qu’il puisse exister un lien profond entre l’activité d’un mathématicien et celle d’un artiste est généralement déconcertante pour les non-mathématiciens. Nombreux sont ceux qui ne retiennent des mathématiques que l’idée d’une pratique technique et aride, où le raisonnement logique domine. Cela semble n’avoir rien en commun avec l’émotion, la créativité et la beauté, toutes choses que le poète, le musicien, le peintre ou d’autres artistes mettent en avant quand ils parlent de leurs travaux.


Pourtant, les mathématiciens témoignent d’expériences émotionnelles intenses parfaitement comparables à celles qu’éprouve un artiste. Le besoin de faire des mathématiques, la fascination esthétique qu’elles engendrent, qu’elles soient pures ou appliquées aux sciences comme la physique théorique, sont aussi impérieux et irrésistibles que ceux à l’origine des œuvres d’artistes comme Hölderlin, Léonard de Vinci ou Bach.

Source : futura-sciences.com

L'impact des loisirs

En 2008, l’enquête de la DEPP, Division Evaluation Prospective et Pilotage, chez des enfants de 11 ans, ne révélait pas d’impact des loisirs, mêmes fréquents sur les performances scolaires et cognitives. Mais depuis, les technologies du numérique ont explosé et envahi le quotidien. La DEPP a réalisé une nouvelle enquête en 2011 sur un large échantillon représentatif de 27 000 adolescents français (14 ans et demi) en classe de 3e de collège. De nombreux tests ont été utilisés : deux tests de lecture/compréhension, douze tests de maths, un test de mémoire, etc... Les analyses montrent qu’il n’y a pas de différences statistiquement significatives entre les résultats des garçons et ceux des filles. Au quotidien, les deux activités les plus fréquemment pratiquées par ces adolescents sont l’écoute des musiques actuelles (79 %) et téléphoner ou envoyer des SMS (78 %). Vient ensuite la communication par internet avec ses ami(e)s (73 %). La quatrième activité au dessus de 50 % est la navigation sur internet (61 %). Les autres loisirs concernent la téléréalité (42 %), la recherche d’infos people sur internet, les chansons et les films d’action/policier/fantastiques. Le premier loisir non virtuel, les activités sportives n’apparaissent qu’à une fréquence de 26 %.

Les résultats montrent clairement les loisirs positifs ou négatifs pour les performances cognitives scolaires. La lecture est la plus bénéfique, une pratique fréquente est favorable à tous les tests, notamment à la compréhension (+10%) et surtout à l’acquisition de connaissances (+20%). Les jeux vidéo n’ont pas d’influence, on ne remarque aucune amélioration pour le raisonnement, ce qui infirme l’hypothèse de transfert de la pratique des jeux vidéo sur l’intelligence fluide, comme l’ont supposé certains chercheurs. A l’inverse, jouer aux jeux vidéo (action, combat, plateforme) n’a pas non plus d’incidence négative. Téléphoner très souvent a une incidence mais faible, sauf pour l’acquisition des connaissances de ceux qui téléphonent ou envoient des SMS (-10 %). Mais c’est le visionnage très fréquent des programmes de téléréalité (et également les séries romantiques) qui a l’impact le plus négatif sur les performances cognitives et scolaires, de -11 % pour les maths à -16 % pour les connaissances.
L'influence de la pratique fréquente de certains loisirs n’est pas négligeable. Si on compare le visionnage de programme de téléréalité à la lecture de romans (policiers ou de littérature), la différence est de 35 % pour les connaissances scolaires (mémoire encyclopédique). La raison principale est la richesse de vocabulaire : 1000 mots dans des livres, 4000 dans les magazines scientifique, 900 dans les bandes dessinées, 600 dans les émissions populaires en prime time pour les adultes, 6000 dans un manuel de 6e et 24 000 dans un manuel de 3e.

Source : cahiers-pedagogiques.com

Ceux qui vivent les maths comme on respire

COMMENT J'AI DÉTESTÉ LES MATHS, documentaire d'Olivier PEYON :
Prenant joyeusement le contrepied de son titre, ce documentaire parle avec passion de l'amour des maths et va vous faire regretter d'être passé à côté. Passion, c'est bien le mot qui convient à ceux qui vivent les mathématiques comme nous respirons. Ces gens dont l'univers contenait déjà un sixième élément avant même que la science fiction n'ait inventé le cinquième. Durant trois ans, Olivier Peyon est allé les traquer un peu partout dans le monde, ces grands curieux insatiables. Ils expliquent l'importance de la recherche fondamentale, la nécessité de ne pas toujours vouloir être dans le productif, le lucre, de prendre le temps de rêver.


COMMENT J'AI DÉTESTÉ LES MATHS - Bande-annonce... par NoPopCorn
Lire la critique sur cinemas-utopia.org/bordeaux/

Le vendredi 13 est un jour particulier

Les mathématiques appliquées au calendrier indiquent que le 13 du mois tombe un tout petit peu plus fréquemment un vendredi que n'importe quel jour de la semaine. Sur 4 000 ans, il y a 6 880 vendredis 13 contre 6 840 jeudis 13 (ou 6 850 lundis ou mardis 13). Il a été possible de démontrer qu'il y avait forcément au moins un vendredi 13 par an, et qu'il ne pouvait pas y en avoir plus de trois. Et il y a en trois si et seulement si le premier jour de l'année est un jeudi pour une année non bissextile comme en 2009 et un dimanche pour une année bissextile.

La mécanique du calendrier fait qu'en 2009 deux vendredis 13 se sont succédés dans deux mois consécutifs, février et mars, et un troisième en novembre. Situation déjà connue en 1998. Et qui se reproduira en 2015, puis 2026. 2010 et 2011 n'ont eu respectivement qu'un vendredi 13, 2012 en a eu trois, en janvier, avril et juillet et en 2013, on a eu 2 vendredis 13, en septembre et décembre. 21 vendredis 13 sont dénombrés, de 2009 à 2019. Toujours grâce aux mathématiques, il a été calculé que les intervalles de jours entre deux vendredis 13 étaient codifiés. Ils sont de 27, 90, 181, 244, 272, 335 ou 426 jours. Donc deux vendredis 13 peuvent être séparés par une durée supérieure à une année. Ce qui s'était produit du 13 août 1999 au 13 octobre 2000.

Source : Le Figaro

2 Mooc de Cédric Villani

En 2014, des élèves et des étudiants de première et deuxième années de licence auront comme professeur Cédric Villani. Le spécialiste de l'analyse mathématique, médaillé Fields en 2010, a décidé de produire deux MOOC (Massive Open Online Courses) : le premier à destination des collégiens et lycées et le second "Nord-Sud" créé en collaboration avec des collègues sénégalais. Pour assurer le succès de France Université Numérique, Cédric Villani n’a qu’un seul mot d’ordre : "avancer résolument".


Un MOOC pour initier les lycéens et les... par fr-universite-numerique

Les mathématiques et le trafic

Beaucoup de nos auditeurs sont peut-être, en ce moment même, bloqués dans les embouteillages qui sévissent dans de nombreuses villes aux heures de pointe. Cédric Villani, est-ce que les mathématiques peuvent faire quelque chose pour les aider ?



Un premier réflexe de bon sens serait de se dire qu'il suffit d'améliorer les transports en commun. Mais ce n'est pas si simple, comme le prouve la mésaventure qui a frappée la Ville de Nice récemment : afin de réduire les embouteillages, la municipalité a augmenté considérablement la fréquence des tramways. Résultat : la ville s'est retrouvée encore bien plus congestionnée qu'avant. Cela semble complètement illogique, on ne voit pas comment cela peut être mis en équations ! Et pourtant c'est un phénomène bien connu des mathématiciens : parfois les transports jouent de sacrés tours. Il y a ce que l'on appelle le Paradoxe de Braess : il n'est pas rare que l'ouverture d'une nouvelle voie dans un réseau urbain entraîne un ralentissement du trafic. A l'inverse, on peut parfois rendre le trafic plus fluide en fermant certaines voies bien choisies : cela a été observé par exemple dans des situations concrètes a Séoul, Stuttgart ou New York...

Pour modéliser le trafic autoroutier, on utilise parfois de la mécanique des fluides, assimilant les voitures à des éléments de fluides. Enfin des outils statistiques sont appliqués au traitement du signal, par exemple pour intégrer les données de circulation captées un peu partout dans le réseau.

Chaos, une aventure mathématique

CHAOS est un film mathématique constitué de neuf chapitres de treize minutes chacun. Il s'agit d'un film tout public autour des systèmes dynamiques, de l'effet papillon et de la théorie du chaos.

La treegonometry, calculs pour Noël

Deux étudiants de l’Université de Sheffield en Grande-Bretagne, Nicole Wrightham et Alex Craig mis au point trois formules mathématiques permettant de trouver le juste équilibre entre la quantité de décorations nécessaires et la taille de l’arbre.

Pour déterminer le nombre de boules nécessaires, il suffit de diviser par 20 la racine carrée de 17, puis de multiplier le résultat par la taille du sapin en centimètres.

Pour connaître la longueur idéale des guirlandes électriques, il faut multiplier π par la taille du sapin. Concernant les guirlandes ordinaires, il faut multiplier π par 13, diviser le résultat par 8 et ensuite multiplier par la hauteur de l’arbre.

Pour savoir quelle taille d’étoile convient le mieux pour le haut de votre sapin, il suffit de diviser la taille de l’arbre par 10.

Nombre de boules = ( √17 x Hauteur de l'arbre ) / 20

Longueur de guirlandes = ( 13 x Pi x Hauteur de l'arbre ) / 8

Longueur de guirlandes électriques = Pi x Hauteur de l'arbre

Hauteur de l'étoile ou fée ( en cm ) = Hauteur de l'arbre / 10

Un arbre de 180 cm nécessitera 37 boules, 919 cm de guirlandes, 565 cm de guirlandes lumineuse et une étoile de 18 cm.

Voici un calculateur en ligne : shef.ac.uk

Toutes les sciences sont humaines

Extrait de l'interview de Cédric Villani, mathématicien français, directeur de l'Institut Henri-Poincaré, publié sur le site lesechos.fr

" Toutes les sciences sont humaines parce que faites par des humains. Je dis souvent que les mathématiques partent de questionnements qui nous sont naturels mais leur appliquent un mode de raisonnement qui l'est moins. Les êtres humains sont faits pour fonctionner à base d'émotions, parce qu'elles sont plus efficaces que le raisonnement pour assurer la survie face au danger. Il faut faire un effort - un effort qui s'apprend -pour conduire un raisonnement logique qui peut être très complexe. Ce travail de structuration est au coeur de la démarche scientifique. On voit souvent la science comme une accumulation sans fin de faits. Mais, il y a cent ans, Henri Poincaré le disait déjà : « On fabrique la science avec des faits comme une maison avec des pierres, mais la science n'est pas plus un amas de faits que la maison un amas de pierres. "

Des maths pour spéculer

En principe, les marchés financiers devraient être des outils de partage des risques, donc utiles à l’économie réelle. De même la titrisation des crédits immobiliers, encadrée et gérée avec une grande prudence, devait permettre de relancer l’industrie américaine du bâtiment avec des risques limités et contrôlés. Mais la gestion d’avoirs essentiellement immatériels, les exigences de bénéfices rapides imposées par certains actionnaires, et la pratique des bonus démesurés versés chaque année aux traders incitent à des comportements nuisibles à l’économie et encore plus grave, désastreux pour les familles pauvres.

L’émission de produits financiers complexes, comme les subprimes, est précédée d’études théoriques qui utilisent des concepts mathématiques élaborés. Ces outils mathématiques devraient servir à modéliser l’évolution des prix de marché d’actifs liquides, à établir des prix de transaction équitables pour certaines options, et à construire des stratégies efficaces de gestion de certains risques. Aussi les mathématiciens enseignent des théories mathématiques qui servent en gestion de produits financiers. Les scientifiques ont un devoir d’alerte quand ils peuvent mettre en évidence un danger collectif, un dévoiement de leurs recherches et des conséquences de leurs enseignements. A cet égard, les mathématiciens ont une responsabilité particulière. L’idée commune au sujet des mathématiques est qu'elles sont abstraites, sans rapport avec le monde réel. La finance, la physique, l’informatique, fournissent des contre-exemples. Bien au contraire, les mathématiques offrent une puissance de modélisation indispensable pour traiter des risques encourus. Les outils les plus sophistiqués de la théorie des probabilités permettent de prendre en compte les incertitudes de modélisation, ou de simulation numérique, de phénomènes aussi complexes que le repliement de protéines, l’évolution de fissures dans des cuves de réacteurs nucléaires, le réchauffement climatique, les effets sur l’économie mondiale d’une taxe Tobin sur les flux financiers. Exprimés sous forme de modèles mathématiques et d’équations, les risques deviennent, au moins en partie, objectifs et quantifiables. Le pouvoir politique dispose alors d’informations utiles pour que la minimisation des risques, plutôt que la maximisation des profits, soit un objectif prioritaire.

Source : images.math.cnrs.fr

Quelques mois pour raviver un volcan endormi

Une chambre magmatique est le grand réservoir de lave, enfoui à plusieurs kilomètres de profondeur sous un volcan, qui l'alimente en roche en fusion. Jusqu'à présent, les volcanologues imaginaient qu'elle se refroidissait en une pâte extrêmement visqueuse, jusqu'à ce qu'une nouvelle lave montant des entrailles de la Terre la fluidifie en la chauffant par contact thermique. Selon cette hypothèse, il fallait plusieurs milliers d'années pour que la chaleur se transmette à l'intégralité du réservoir, sortant le volcan de sa léthargie.

Selon le modèle mathématique mis au point par Alain Burgisser du CNRS et son collaborateur américain Georges Bergantz , le réchauffement se déroule en trois étapes. Lorsque de la lave fraîche et chaude remonte des profondeurs et arrive sous la chambre, elle fait fondre la lave visqueuse qui constitue les racines du réservoir ; cette lave nouvellement fondue devient alors légère et entame une ascension à travers la chambre, forçant le reste de la pâte visqueuse à se mélanger. C'est ce processus de mélange qui permet à la chaleur de diffuser cent fois plus vite dans la chambre que les volcanologues ne le prévoyaient. En fonction de la taille de la chambre et de la viscosité des roches qu'elle contient, quelques mois peuvent alors suffire à raviver son activité.

Les deux chercheurs ont vérifié la validité de leur modèle sur l'éruption du Pinatubo aux Philippines, en mars 1991, qui avait causé 1000 morts et l'évacuation de deux millions de personnes. Les secousses sismiques précédant l'éruption avaient indiqué l'arrivée de lave fraîche sous le réservoir refroidi. Les deux scientifiques ont réussi à reproduire approximativement les durées entre ces signaux d'alarme et les éruptions. Pour le Pinatubo, le modèle mathématique a prédit que 20 à 80 jours suffisaient pour remobiliser la chambre sous-jacente, alors que la théorie classique envisageait, elle, 500 ans. Dans la réalité, deux mois avaient séparé les tremblements de terre de l'explosion de ce volcan.

Pour plus d'informations, on peut consulter le site du CNRS

Une image géométrique qui évoque une côte marine

Il y a tout juste un mois, le mathématicien franco-américain Benoît Mandelbrot est mort à Cambridge, dans le Massachussets aux Etats-Unis. Durant sa carrière, il a ouvert de nouvelles perspectives à l'application des mathématiques, en travaillant sur les fractales, ces figures mathématiques correspondant à une géométrie de la nature. Il a toujours pratiqué une approche scientifique très personnelle, en conservant toute sa liberté.

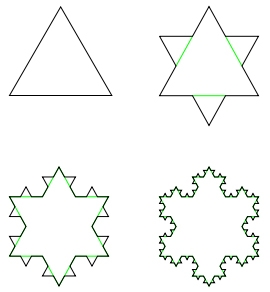
Imaginons un triangle sur les côtés duquel on trace trois petits triangles, sur les côtés desquels on trace trois triangles, et ainsi de suite... On obtient une courbe, dite de Koch, dont les excroissances se ressemblent, qu'on les regarde de près ou de loin. Une image géométrique qui évoque une côte marine comme celle de Bretagne.

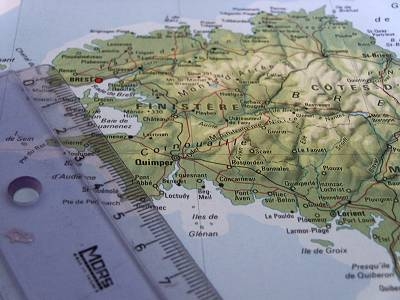
Qu'on l'observe depuis un satellite, d'un avion ou sous ses pieds, la côte de Bretagne semble toujours égale à elle-même. Quelle est la longueur de la côte bretonne ? Cette côte présente de très nombreuses circonvolutions avec quelques grands golfes qui contiennent des golfes plus petits et des criques de toutes tailles, ainsi que des promontoires plus ou moins découpés. Sur le terrain nous observerons en outre des détails de plus petite taille qui ne peuvent pas être représentés sur la carte et qui sont dus aux irrégularités des rochers. Comme le flocon de von Koch, la longueur de la côte de la Bretagne est, en toute rigueur, infinie. Ce travail semble avoir été à l'origine des recherches de Mandelbrot sur l'utilisation des fractales pour obtenir des images de synthèse de paysages.

Pour plus d'informations on peut consulter le site futura-sciences.com

C'est dans la profusion du réel que Mandelbrot a cherché, durant 50 ans, des formules en termes mathématiques. L'ordinateur est venu le seconder dans cette tâche. Grâce à cet outil, les possibilités de dessiner de façon systématique et automatique ce que la main ne pourrait obtenir, le visuel a été réintroduit dans les mathématiques. Le chou romanesco ressemble au brocoli par sa couleur vert pomme et au chou-fleur par sa forme compacte, mais est constitué d'un ensemble de florettes pyramidales disposées en couronnes spiralées dont la forme géométrique, dite fractale est très particulière.

Pour en savoir plus, on peut consulter le site liberation.fr ou slate.fr